二等辺三角形の領域を見つける方法

数学、およびジオメトリは、特にあなたが現在の大人の90%が実際的なアプリケーションを見つけていない人生で数え切れないほど多くの数式を学ぶようにするので、学生の世論調査、最も愛されていないレッスンのいずれか、そしてすべて。しかし、1分間、式を学び、問題を解決し、生命の中で私たちにとって有用であるという事実ではなく、思考と論理を発達させるために方程式を作ります。古代ギリシャの賢者でさえ、人間の知性は数理科学の知識によって測定できると語った。また、二等辺三角形の数式の適用について知りたがっているので、私たちは手を携えて記事全体を読んでいます。
あなたがどのように見つけるのかという質問に答える前に二等辺三角形の面積を計算し、数式と計算が与えられた記事の実用的な部分に行くと、私たち自身のためのコンセプトを示すことができます。二等辺三角形は、3つの辺のうちの2つが長さが等しく、横辺と呼ばれる三角形である。すべての辺が等しい正三角形の場合、二等辺三角形が正しいとみなされるときは二等辺三角形と見なされますが、逆の場合は偽です。
三角形の辺を指定する必要があります。下の図のように、このようにします。a - sides、b-base、およびh-height。
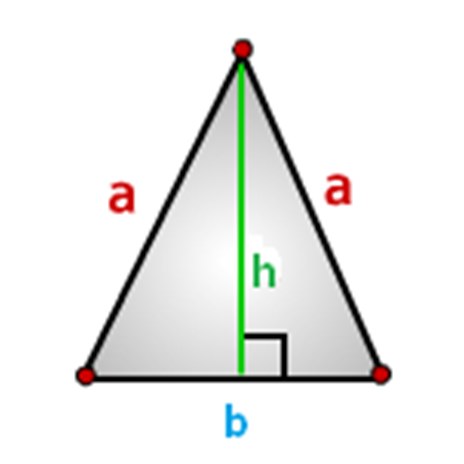
二等辺三角形、数式の面積を計算する方法。
高さ、辺、角度の表記をした後、問題を解決することができます。
まず、私たちが知っていることを決定します。
高さと底の場合 - 古典的な数式(* - 倍数記号):
S = 1/2 * b * h
たとえば、h = 16、b = 18の数字を代用すると、次のようになります。
S = 1/2 * 18 * 16 = 9 * 16 = 144;
二等辺三角形の面積は、S = 144cm2
私たちを助ける他の数式があります二等辺三角形の面積を知る方法。そのような式の1つは、ヘロンの方法です。複雑な数式を書くことはしません。
S =¼b√4* a2-b2
bが基底であり、 - 等辺であることは明らかである。この式は、高さが不明な場合に適しています。
値をa = 6、b = 3とすると、次のようになります。
S = 1/4 * 3√4* 62-32 = 3/4√144-9= 3/4 * 9 = 8,7
三角形の辺に等しい面積と辺の間の角度を計算するために使うことができます:
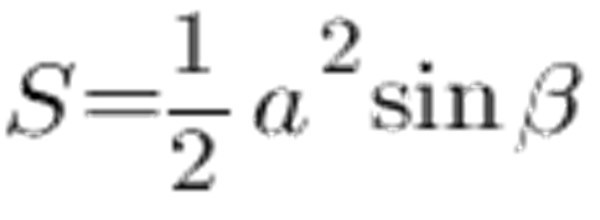
正弦表によれば、45°の角度は0.7071に等しく、aの面は6cmとすると、次のようになります。
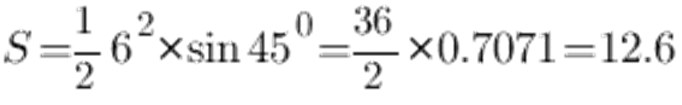
結果として、二等辺三角形の面積は12.6cm 2である。
面積を計算する方法もあります。二等辺三角形に関して含め、彼らは非常に複雑であり、上記のタイプの複雑な数学計算、の「基本」という概念には適用されません。そして、経験でも、教師を理解していない事柄について話す - それだけの価値はありません。
それで、あなたは救済のため息を吹き込むことができます二等辺三角形の領域を見つける際の幾何学的な小さなコースが完成したものとみなされ、記事を読んだ結果得られる知識は「5」によって学習されます。